1. 문제 설명

2. 문제 조건

3. 문제 해결 아이디어
- 적절한 높이를 찾을 때까지 이진 탐색을 수행하여 높이 H를 반복해서 조정
- 현재 이 높이로 자르면 조건을 만족할 수 있는가?를 확인한 후 탐색 범위를 좁히기
- 절단기의 높이는 0~10억까지 정수 중 하나
- 큰 범위는 대부분 이진 탐색
- 과정을 반복하면서 얻을 수 있는 떡의 길이 합이 나올 동안 중간점의 값을 기록한다.
[Step 1]

- 시작점: 0, 끝점: 19, 중간점: 9(자르고자 하는 높이)
- 이때 필요한 떡의 크기: M = 6이므로, 결과 저장
- 탐색 범위는 0~19이다 중간점은 나누면 9가 될 것이다.
- 잘린 떡의 길이는 모두 25가 나온다. 중간점의 9를 기록하고 중간점을 오른쪽으로 높이면서 또 확인한다.
[Step 2]

- 시작점: 10, 끝점: 19, 중간점: 14
- 필요한 떡의 길이가 M = 6이므로 (잘린 떡은 9) 결과 14를 기록하고 오른쪽으로 한칸 또 옮긴다.
- 시작점을 중간점보다 1큰걸로 위처럼 설정한다.
[Step 3]

- 이경우 만족하지 못하므로 결과를 저장하지 않는다.
- 다시 끝점을 중간점의 왼쪽인 16으로 바꾼다.
[Step 4]
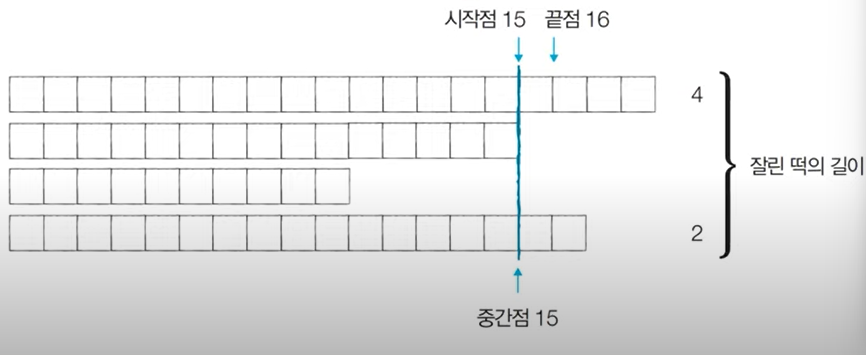
- 시작점: 15, 끝점: 16, 중간점: 15
- 잘린 떡이 6이 맞으므로 현재의 중간점의 결과를 저장한다.
- 그리고 종료한다.
4. 소스코드
#떡의 개수(n)와 요청한 떡의 길이(m)을 입력
n, m = list(map(int, input().split(' ')))
#각 떡의 개별 높이 정보를 입력
array = list(map(int, input().split()))
#이진 탐색을 위한 시작점과 끝점 설정
start = 0
end = max(array)
#이진 탐색 수행(반복적)
result = 0
while(start <= end):
total = 0
mid = (start + end) // 2
for x in array:
#잘랐을 때의 떡의 양 계산
if x > mid:
total += x - mid
#떡의 양이 부족한 경우 더 많이 자르기(왼쪽 부분 탐색)
if total < m:
end = mid - 1
#떡의 양이 충분한 경우 덜 자르기(오른쪽 부분 탐색)
else:
result = mid #최대한 덜 잘랐을 때가 정답이므로
start = mid + 1
#정답 출력
print(result)- 매번 mid값을 설정하게 해주고 x(현재 떡이) mid보다 클 경우
- 높이를 줄이고 늘리는 과정을 반복한다.
'CodingTest > 이진 탐색' 카테고리의 다른 글
| 정렬된 배열에서 특정 수의 개수 구하기 (0) | 2022.07.12 |
|---|---|
| 값이 특정 범위에 속하는 데이터 개수 구하기 (0) | 2022.07.12 |
| 이진 탐색 알고리즘 이론 (0) | 2022.07.12 |